发表于 | 分类于

题目

给定一个字符串 s，计算具有相同数量0和1的非空(连续)子字符串的数量，并且这些子字符串中的所有0和所有1都是组合在一起的。

重复出现的子串要计算它们出现的次数。

示例 1 :

输入: “00110011”
输出: 6
解释: 有6个子串具有相同数量的连续1和0：“0011”，“01”，“1100”，“10”，“0011” 和 “01”。

请注意，一些重复出现的子串要计算它们出现的次数。

另外，“00110011”不是有效的子串，因为所有的0（和1）没有组合在一起。

示例 2 :

输入: “10101”
输出: 4
解释: 有4个子串：“10”，“01”，“10”，“01”，它们具有相同数量的连续1和0。
注意：

s.length 在1到50,000之间。
s 只包含“0”或“1”字符。

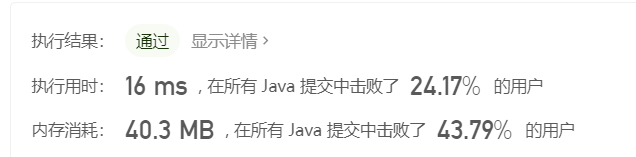
按照字符连续数目分组

对于字符串s="00011100", 我们可以构建新的数组counts, 记录连续字符的数目, 即counts={3, 3, 2}, 只要遍历counts数组, 将相邻数对的最小值相加即可.

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int countBinarySubstrings(String s) {
        List<Integer> counts = new ArrayList<>();
        int len = s.length(), cnt = 1;
        char c = s.charAt(0);
        for (int i = 1; i < len; i++) {
            if (s.charAt(i) == c) {
                cnt++;
            } else {
                counts.add(cnt);
                cnt = 1;
                c = s.charAt(i);
            }
        }
        counts.add(cnt);
        int res = 0;
        for (int i = 0; i < counts.size() - 1; i++) {
            res += Math.min(counts.get(i), counts.get(i + 1));
        }
        return res;
    }
}

image-20200810125052901

发表于 | 分类于

题目

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长（长度 ~= 500,000），而 s 是个短字符串（长度 <=100）。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，”ace”是”abcde”的一个子序列，而”aec”不是）。

示例 1:
s = “abc”, t = “ahbgdc”

返回 true.

示例 2:
s = “axc”, t = “ahbgdc”

返回 false.

双指针

用指针i指向字符串s的元素, 指针j指向字符串t的元素.

遍历字符串t, 如果i和j指向的元素相等, 则i++, 以便查看之后的元素.

当字符串t遍历结束后, 如果字符串s也遍历完成, 即i==s.length(), 那么说明字符串s就是字符串t的子串.

幻灯片1

代码如下

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean isSubsequence(String s, String t) {
        if (s.length() > t.length()) return false;
        int i = 0, j = 0;
        while (i < s.length() && j < t.length()) {
            if (s.charAt(i) == t.charAt(j)) i++;
            j++;
        }
        return i == s.length();
    }
}

image-20200727131740343

发表于 | 分类于

题目

给定一个包含非负整数的 m x n 网格，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例:

1
2
3
4
5
6
7
8
输入:
[
  [1,3,1],
  [1,5,1],
  [4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。

动态规划

非常典型的动态规划, 用dp[i][j]表示当前路径的最小总和, 那么动态转移方程为:

MommyTalk159547074613187

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int minPathSum(int[][] grid) {
        int n = grid.length, m = grid[0].length;
        if (m == 0 || n == 0) return 0;
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                dp[i][j] += grid[i][j];
                if (i == 0 && j > 0) dp[i][j] += dp[0][j - 1];
                else if (j == 0 && i > 0) dp[i][j] += dp[i - 1][j];
                else if (i != 0 && j != 0) {
                    dp[i][j] += Math.min(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[n - 1][m - 1];
    }
}

image-20200723101953872

发表于 | 分类于

题目

给定一个整数 n，生成所有由 1 … n 为节点所组成的 二叉搜索树

image-20200721092547034

递归

遍历1...n中的所有元素, 以当前元素为根结点. 计算所有可能的左子树和右子树, 并将所有左子树-右子树组合拼接到根结点上.

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if (n == 0) {
            return new ArrayList<TreeNode>();
        }
        return generateTrees(1, n);
    }

    public List<TreeNode> generateTrees(int start, int end) {
        ArrayList<TreeNode> roots = new ArrayList<>();
        if (start > end) {
            roots.add(null);
            return roots;
        }
        for (int i = start; i <= end; i++) {
            List<TreeNode> leftTrees = generateTrees(start, i - 1);  // 获取所有可能的左子树
            List<TreeNode> rightTrees = generateTrees(i + 1, end);  // 获取所有可能的右子树
            
            // 遍历所有左子树和右子树的组合, 拼接到根结点上
            for (TreeNode leftTree : leftTrees) {
                for (TreeNode rightTree : rightTrees) {
                    TreeNode root = new TreeNode(i, leftTree, rightTree);
                    roots.add(root);
                }
            }
        }
        return roots;
    }
}

image-20200721092906650

发表于 | 分类于

题目

在整数数组 nums 中，是否存在两个下标 i 和 j，使得 nums [i] 和 nums [j] 的差的绝对值小于等于 t ，且满足 i 和 j 的差的绝对值也小于等于 ķ 。

如果存在则返回 true，不存在返回 false。

示例 1:

输入: nums = [1,2,3,1], k = 3, t = 0
输出: true

示例 2:

输入: nums = [1,0,1,1], k = 1, t = 2
输出: true

示例 3:

输入: nums = [1,5,9,1,5,9], k = 2, t = 3
输出: false

平衡二叉树/红黑树

Java中的Treeset内部是由红黑树实现的. Treeset.ceiling函数可以寻找特定节点的中序后继, Treeset.floor函数可以寻找特定节点的中序前驱.

  • 初始化一颗空的红黑树tree
  • 遍历整个数组, 对于每一个元素nums[i]:
    • 在tree上查找nums[i]的后继s(大于等于nums[i]的最小的数), 如果s-nums[i]<=t, 则返回true
    • 在tree上查找nums[i]的前驱g(小于等于nums[i]的最大的数), 如果nums[i] - g<=t, 则返回true
    • 在tree中插入nums[i]
    • 如果tree的大小超过了k, 则移除最早加入tree的那个数(nums[i-k])

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
        TreeSet<Integer> tree = new TreeSet<>();
        for (int i = 0; i < nums.length; i++) {
            Integer s = tree.ceiling(nums[i]); // 寻找当前元素的后继
            Integer g = tree.floor(nums[i]);  // 寻找当前元素的前驱
            
            if (s != null && s <= t + nums[i]) return true;
            if (g != null && nums[i] <= t + g) return true;
            
            tree.add(nums[i]);
            if (tree.size() > k) {
                tree.remove(nums[i - k]);
            }
        }
        return false;
    }
}

image-20200720181700539

发表于 | 分类于

题目

给定一个已按照升序排列 的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。

说明:

返回的下标值（index1 和 index2）不是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。

示例:

输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

双指针

指针i指向第一个元素, 指针j指向最后一个元素.

计算两个指针对应元素之和sum:

  1. 如果sum大于target, 则需要减小元素之和, 那么j--
  2. 如果sum小于target, 则需要增加元素之和, 那么i++
  3. 如果sum等于targe, 则直接返回i+1和j+1(题目要求下标从1开始)

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int[] twoSum(int[] numbers, int target) {
        int i = 0, j = numbers.length - 1;
        while (i < j) {
            int sum = numbers[i] + numbers[j];
            if (sum < target) i++;
            if (sum > target) j--;
            if (sum == target) break;
        }
        return new int[]{i + 1, j + 1};
    }
}

image-20200720083246426

发表于 | 分类于

题目

给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。

示例 1:

输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出: true
示例 2:

输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出: false

动态规划

要判断s3是否由s1和s2交错而成的, 首先看长度.

如果|s1|+|s2| != |s3|, 那么说明s3不是由s1和s2交错而成的.

假设dp[i][j]表示s1的前i个元素和s2的前j个元素能否构成s3的前i+j个元素.

那么dp[i][j]取决于dp[i-1][j], dp[i][j-1]以及对应位置的元素是否相等.

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int n = s1.length(), m = s2.length(), t = s3.length();
        if (n + m != t) return false;
        boolean[][] dp = new boolean[n + 1][m + 1];
        dp[0][0] = true;
        for (int i = 0; i <= n; i++) {
            for (int j = 0; j <= m; j++) {
                int p = i + j - 1;
                if (i > 0) {
                    dp[i][j] = dp[i][j] || (s1.charAt(i - 1) == s3.charAt(p) && dp[i - 1][j]);
                }
                if (j > 0) {
                    dp[i][j] = dp[i][j] || (s2.charAt(j - 1) == s3.charAt(p) && dp[i][j - 1]);
                }
            }
        }
        return dp[n][m];
    }
}

image-20200718092411513

发表于 | 分类于

题目

给定一个无向图graph，当这个图为二分图时返回true。

如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合，一个来自B集合，我们就将这个图称为二分图。

graph将会以邻接表方式给出，graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边： graph[i] 中不存在i，并且graph[i]中没有重复的值。

image-20200716102844735

注意:

graph 的长度范围为 [1, 100]。
graph[i] 中的元素的范围为 [0, graph.length - 1]。
graph[i] 不会包含 i 或者有重复的值。
图是无向的: 如果j 在 graph[i]里边, 那么 i 也会在 graph[j]里边。

思路

对图中的节点进行染色. 以任意一个节点开始, 将其染成红色, 然后对图进行遍历, 将其邻居染成黑色. 然后将黑色的邻居染成红色. 如果可以染色成功, 说明这个图是二分图, 两个集合分别是黑色节点和红色节点. 如果染色不能成功, 说明该图不是二分图.

遍历图的思路主要有两种, 分别是深度优先搜索DFS和广度优先搜索BFS.

深度优先搜索DFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    // 染色的标记
    private static int UNCOLOR = 0;
    private static int RED = 1;
    private static int BLACK = 2;

    // 标记节点是否染色
    private int[] colorFlag;

    // 是否符合题目要求
    boolean valid = true;

    public boolean isBipartite(int[][] graph) {
        colorFlag = new int[graph.length];
        for (int i = 0; i < graph.length; i++) {
            // 因为图不一定是连通的, 所以需要以所有为染色的节点为起点去染色
            if (colorFlag[i] == UNCOLOR) {
                dfs(i, RED, graph);
            }
        }
        return valid;
    }

    private void dfs(int node, int color, int[][] graph) {
        // 对当前节点进行染色
        colorFlag[node] = color;
        // 确定相邻节点需要染的颜色
        int colorOfNeighbour = color == RED? BLACK: RED;
        // 遍历相邻的节点
        for (int neighbour: graph[node]) {
            if (colorFlag[neighbour] == UNCOLOR) {
                dfs(neighbour, colorOfNeighbour, graph);
                // 通过上面的dfs, 如果不是二分图, 则直接返回
                if (!valid) {
                    return;
                }
            } else if (colorFlag[neighbour] != colorOfNeighbour) {
                // 如果相邻节点已经有颜色, 而且和确定要染的颜色不一样的话, 则说明不是二分图
                // 不满足题目要求
                valid = false;
                return;
            }
        }
    }
}

image-20200716103505511

广度优先搜索BFS

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    // 染色的标记
    private static int UNCOLOR = 0;
    private static int RED = 1;
    private static int BLACK = 2;

    // 标记节点是否染色
    private int[] colorFlag;

    public boolean isBipartite(int[][] graph) {
        colorFlag = new int[graph.length];
        for (int i = 0; i < graph.length; i++) {
            // 因为图不一定是连通的, 所以需要以所有为染色的节点为起点去染色
            if (colorFlag[i] == UNCOLOR) {
                Queue<Integer> queue = new LinkedList<>();
                // 先将第一个节点入队
                queue.offer(i);
                colorFlag[i] = RED;
                while (!queue.isEmpty()) {
                    // 队首节点出队
                    int node = queue.poll();
                    // 确认出队节点的相邻节点需要染的颜色
                    int colorOfNeighbour = colorFlag[node] == RED? BLACK: RED;
                    // 遍历出队节点的所有相邻节点
                    for (int neighbour: graph[node]) {
                        if (colorFlag[neighbour] == UNCOLOR) {
                            // 如果当前相邻节点还没有染色
                            // 入队
                            queue.offer(neighbour);
                            // 染色
                            colorFlag[neighbour] = colorOfNeighbour;
                        } else if (colorFlag[neighbour] != colorOfNeighbour) {
                            // 如果当前相邻节点已染色, 且与需要染的颜色不一样
                            return false;
                        }
                    }
                }
            }
        }
        return true;
    } 
}

image-20200716105628992

发表于 | 分类于

题目

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

image-20200715161855733

动态规划

对于有序序列1...n, 假设以数字j为根, 那么构造搜索二叉树的时候, 序列1...(j-1)为左子树的元素, 序列(j+1)..n则为右子树的元素.

假设dp[j]为长度为j的序列所能组成的二叉搜索树数目.

那么由图可知, 假设i为序列的总长度, 则有dp[j]=dp[j-1]*dp[i-j]

image-20200715163040993

对于长度为i的序列, 进行j=1..i的遍历, 累计构造出来的子树的数量即可. 代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }
        return dp[n];
    }
}

image-20200715163222316

发表于 | 分类于

题目

给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。

相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。

例如，给定三角形：

image-20200714105032667

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

动态规划

假设dp[i][j]是处于位置(i, j)时的最小路径总和.

由于位置(i, j)只能从位置(i-1,j-1)和位置(i-1, j)过来, 那么可以很容易的知道动态转移方程为:

dp初始化

对dp所有元素初始赋值为Integer.MAX_VALUE, 方便进行比较最小值.

需要注意的是, dp[i][0]只能从上方转移, 所以初始化的时候需要另外处理.

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[][] dp = new int[n][n];

        // dp初始化
        for (int i = 0; i < n; i++) {
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        dp[0][0] = triangle.get(0).get(0);
        for (int i = 1; i < n; i++) {
            dp[i][0] = triangle.get(i).get(0) + dp[i - 1][0];
        }
        
        for (int i = 1; i < n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + triangle.get(i).get(j);
            }
        }

        int min = Integer.MAX_VALUE;
        for (int j = 0; j < n; j++) {
            if (dp[n - 1][j] < min) {
                min = dp[n - 1][j];
            }
        }
        // for (int i = 0; i < n; i++) {
        //     System.out.println(Arrays.toString(dp[i]));
        // }
        return min;
    }
}

image-20200714105910433