Leetcode-718 最长重复子数组

发表于 | 分类于

题目

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

示例 1:

输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]

输出: 3

解释:
长度最长的公共子数组是 [3, 2, 1]。

说明:

1 <= len(A), len(B) <= 1000
0 <= A[i], B[i] < 100

暴力解法

首先看一下暴力解法.

使用下标i遍历数组A, 使用下标j遍历数组B. 寻找以元素A[i]和B[j]为首的最长公共数组长度$s_{ij}$, 那么全局的最长公共数组长度为

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int findLength(int[] A, int[] B) {
        int s = 0;
        for (int i = 0; i < A.length; i++) {
            for (int j = 0; j < B.length; j++) {
                int k = 0;
                while (i + k < A.length && j + k < B.length 
                       && A[i + k] == B[j + k]) {
                    k++;
                    s = Math.max(s, k);
                }
            }
        }
        return s;
    }
}

时间复杂度为$O(n^3)$

动态规划

在暴力解法当中, 元素A[i]和元素B[j]会进行多次比较. 可以利用动态规划来进行优化, 使得元素A[i]和元素B[j]只会进行一次比较.

令dp[i][j]为元素A[i]和元素B[j]的最长公共重复子数组长度. 那么我们可以知道, 若A[i]==B[j], 则有dp[i][j]=dp[i+1][j+1]+1; 若A[i]!=B[j], 则有dp[i][j]=0. 由于dp[i][j]依赖于dp[i+1][j+1], 所以i和j需要从后往前遍历.

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int findLength(int[] A, int[] B) {
        int m = A.length, n = B.length;
        int[][] dp = new int[m + 1][n + 1];  // default 0
        int s = 0;
        for (int i = m - 1; i >= 0; i--) {
            for (int j = n - 1; j >= 0; j--) {
                if (A[i] == B[j]) {
                    dp[i][j] = dp[i + 1][j + 1] + 1;
                } else {
                    dp[i][j] = 0;
                }
                s = Math.max(s, dp[i][j]);
            }
        }
        return s;
    }
}

滑动窗口

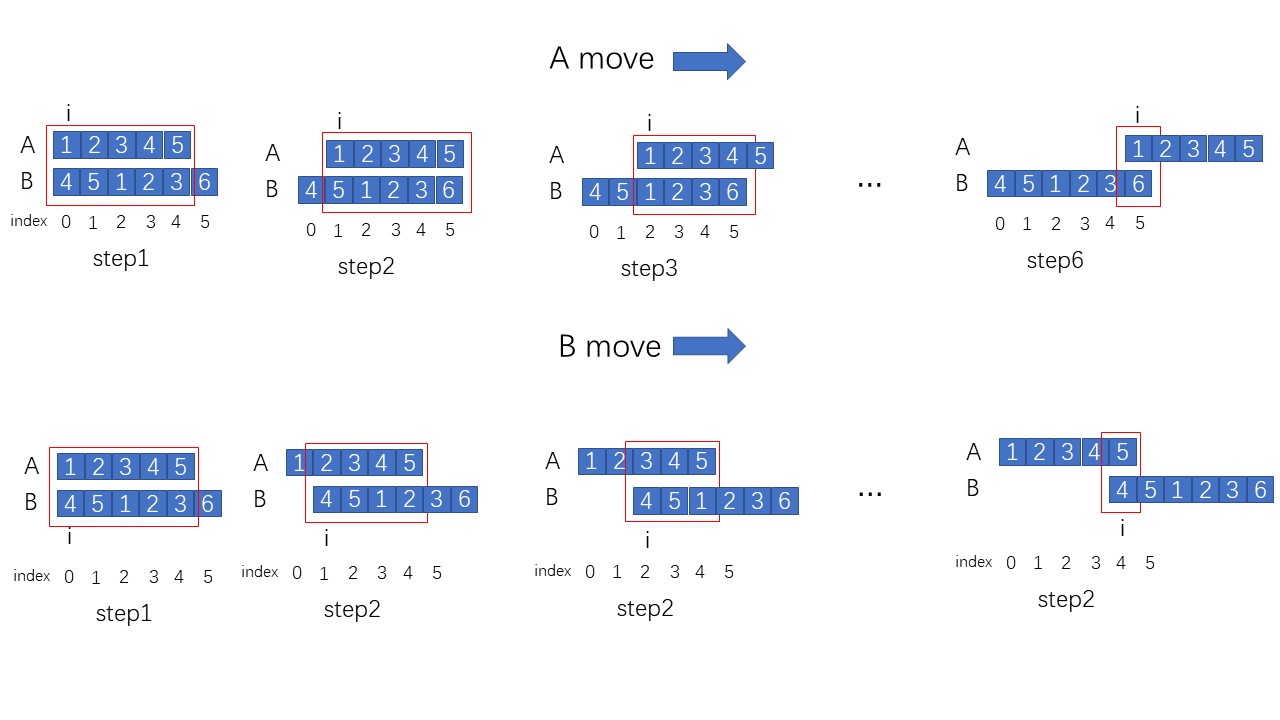
如图所示, 分别枚举数组A向右移动和数组B向右移动的所有情况, 然后计算红框内最大的公共数组长度.

代码如下所示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
    public int findLength(int[] A, int[] B) {
        int m = A.length, n = B.length;
        int s = 0;

        // A move
        for (int i = 0; i < n; i++) {
            int len = Math.min(n - i, m); // 取重叠处的长度
            int tmp = maxLength(A, B, 0, i, len);  // 计算红框处的最大公共子数组长度
            s = Math.max(s, tmp);
        }

        // B move
        for (int i = 0; i < m; i++) {
            int len = Math.min(m - i, n);
            int tmp = maxLength(A, B, i, 0, len);
            s = Math.max(s, tmp);
        }

        return s;
    }

    private int maxLength(int[] A, int[] B, int startA, int startB, int len) {
        int s = 0, k = 0;
        for (int i = 0; i < len; i++) {
            if (A[startA + i] == B[startB + i]) {
                k++;
            } else {
                k = 0;
            }
            s = Math.max(s, k);
        }
        return s;
    }
}